Question

The percentage of women in the United States who will wear a size 6 or smaller is(Round to one decimal place as needed.)

Answer 1

The Normal Distribution

It's a function that represents the distribution of many random variables as a symmetrical bell-shaped graph,

A normal distribution is defined by two parameters: The mean (μ) and the standard deviation (σ).

To calculate probabilities with the normal distribution we use technology in the form of a statistic calculator, an online site, known tools like Excel, etc.

These tools calculate the probability of occurrence of a value less than or equal to X, P(x ≤ X) which is known as the left tail of the bell curve.

It's common for these tools to require the calculation of a so-called z-score:

`z=(X-\mu)/(\sigma)`

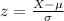
We are given the distribution of the foot lengths of women with a mean of μ = 22.9 cm and a standard deviation of σ = 1.3 cm.

It's required to find the probability of the US women having a shoe size of X = 22.4 cm or smaller.

Calculate the z-score:

`z=(22.4-22.9)/(1.3)=-0.3846`

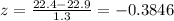
Now we use Excel to calculate P(z ≤ -0.3846) = 0.35027

The percentage is 35.0%