Question

Solve the following system of equations using the substitution method: y= x2 +3x-12 and y=x+3.

Answer 1

Let:

`\begin{gathered} y=x^2+3x-12\text{ (1)} \\ y=x+3\text{ (2)} \\ \end{gathered}`

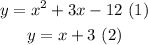
Replacing (1) into (2):

`\begin{gathered} x^2+3x-12=x+3 \\ \text{Subtract (x+3) from both sides:} \\ x^2+3x-12-x-3=0 \\ x^2+2x-15=0 \end{gathered}`

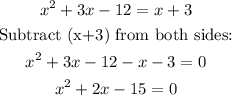
The factors of -15 that sum to 2 are -3 and 5, therefore:

`\begin{gathered} x^2+2x-15=(x-3)(x+5)=0 \\ So\colon \\ x=3 \\ or \\ x=-5 \end{gathered}`

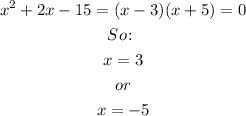
For x = 3:

y = 3² + 3*(3) - 12 = 9 + 9 - 12 = 6

y = (3) + 3 = 6

This solution is correct

For x = -5

y = (-5)² + 3(-5) - 12 = 25 - 15 - 12 = -2

y = (-5) + 3 = -2

This solution is correct as well.

Therefore, the solutions are:

(3,6) and (-5,-2)

or

x = 3 and y = 6

x = -5 and y = -2