ANSWER
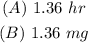
Step-by-step explanation
(A) To find the half-life of the drug, apply the exponential decay formula:
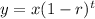
where y = amount remaining
x = initial amount = 225 mg
r = decay rate = 40% = 0.4
t = time elapsed
Substituting the given values into the equation above:
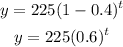
The half-life will occur when the amount of the drug is halved:
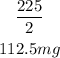
Substitute that for y and solve for t:
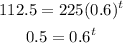
Convert the exponential equation into a logarithmic equation:
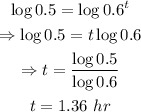
That is the half-life of the drug.
(B) To find the amount of the drug left after 10 hours, substitute 10 for t in the decay equation:
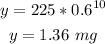
That is the answer.