SOLUTION
Given the question in the question tab, the following are the steps to solve the problem
Step 1: State the formula for probability
Sample Space is the number of letters in MATHEMATICS
Expected outcome is the number of letters which are not vowels in MATHEMATICS

Step 2: Calculate the chance of choosing a paper which is not a vowel
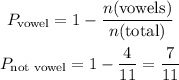
Step 3: Express the odds against the paper having a vowel written on it as a ratio
The outcome of 7/11 expressed as ratio of vowels against total outcome will be:

Hence, the odds against the paper having a vowel written on it as a ratio is 7:4