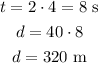A,
The highest point occurs when the vertical velocity is equal to zero.
Then, to find the time needed, we can use the formula below:
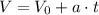
Where V is the final velocity after t seconds, V0 is the initial velocity and a is the acceleration.
So, using V = 0, V0 = 40 m/s and a = -10 m/s² (gravity acceleration), we have:
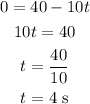
B.
To calculate the horizontal distance traveled in the 4 seconds to reach the maximum height, we can use the formula below:
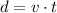
Where d is the distance, v is the horizontal velocity and t is the time.
So, using v = 40 m/s and t = 4 s, we have:
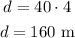
Also, to find the total horizontal distance traveled until the football reaches the ground again, we can use the time of flight as double the time to reach the maximum height: