The width of the rectangle is half its length. Let "x" represent the length of the rectangle, then the width can be expressed as "1/2x"
The perimeter of the rectangle is calculated by adding two times its width and two times its length:
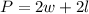
For the given rectangle we know that the perimeter is P=540ft, the length is l=x and the width is w=1/2x. Replace the measures in the formula:
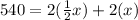
From this expression, you can determine the value of x:
-Solve the multiplications and simplify the like terms
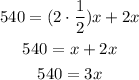
-Divide both sides of the equation by 3 to determine the value of x:
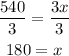
The length of the rectangle is 180ft, the correct option is B.