Question

The normal freezing point of benzene (C6H6) is 5.5 °C. If 22.77 grams of the nonvolatile nonelectrolyte juglone (C10H6O3), are dissolved in 222.3 grams of benzene, what is the freezing point of the resulting solution? Kfp for benzene is 5.12 °C/m. °C

Answer 1

To answer this question, we have to use the equation for cryoscopic descent:

`\Delta T_c=k_(fp)\cdot m`

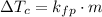
Where ΔTc is the change in the freezing point, kfp is the cryoscopic constant and m is the molality of the solution.

The first step we have to follow is to find the amount of moles of juglone present in the solution. The molar mass of juglone is 174.15g/mol. Divide the mass of juglone in the solution by its molar mass to find the amount of moles present in it:

`(22.77g)/(174.15g/mol)=0.13mol`

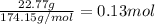
The next step is to find the molality of the solution, to do it divide the amount of moles of juglone (solute) by the kg of benzene (solvent):

`m=(0.13mol)/(0.2223kg)=0.588m`

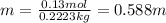
After this, we have to find the change in the freezing point:

`\begin{gathered} \Delta T_c=k_(fp)\cdot m \\ \Delta T_c=5.12\degree C/m\cdot0.588m \\ \Delta T_c=3.01\degree C \end{gathered}`

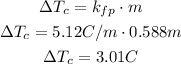
Finally use the change in temperature to find the freezing point of the resulting solution, substract the change in the freezing point to the freezing point of benzene:

`5.5\degree C-3.01\degree C=2.49\degree C`

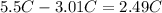
It means that the freezing point of the resulting solution is 2.49°C.