Step-by-step explanation
From the statement, we know that:
0. a guy has two part-time jobs,
,
1. he can work a maximum of 8 hours per day in each job
,
2. he earns r₁ = $25/h in the first job,
,
3. he earns r₂ = $38/h in the second job,
,
4. he wants to earn at least $400 per day.
We define the variables:
• x = time in the first job (in hours),
,
• y = time in the second job (in hours).
Using the data from the statement, we write the following inequalities:
(1) Money from jobs 1 and 2:
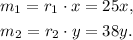
(2) We want to have at least earnings of:
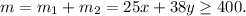
With the restrictions:

(3) Plotting a graph of the region:
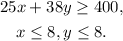
We get the following graph:
Answer
The possible number of hours that he must spend in both works are all the pair of values (x, y) that falls inside the triangle given by the intersection of the regions of the graph: