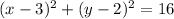Question

Attached is the problem. I know x = 3, y = 2

Answer 1

Step-by-step explanation:

The coordinate of the center is given below as

`\begin{gathered} A=(3,2) \\ A(h,k)=(3,2) \end{gathered}`

From the image below

The general equation of a circle is represented below as

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (h,k)=center \\ r=radius \end{gathered}`

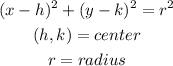
To figure out the value for r, we will use the formula below

`\begin{gathered} r=√((x_2-x_1)^2+(y_2-y_1)^2) \\ x_1=3,x_2=7 \\ y_1=2,y_2=2 \end{gathered}`

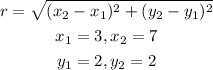
By substituting the values, we will have

`\begin{gathered} r=√((x_2-x_1)^2+(y_2-y_1)^2) \\ r=√((7-3)^2+(2-2)^2) \\ r=√(4^2+0^2) \\ r=√(16) \\ r=4 \\ r^2=16 \end{gathered}`

Hence,

The final answer by substituting the center and the radius will be given below as

`\begin{gathered} (x-h)^(2)+(y-k)^(2)=r^(2) \\ (x-3)^2+(y-2)^2=16 \end{gathered}`

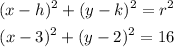
Hence,

The final answer is

`(x-3)^(2)+(y-2)^(2)=16`