(a) No, it does not seem likely that there is a strong association.
Taking, for example, the next values:
HR salary
0 557,500
9 3,750,000
10 556,400
13 20,000,000
47 605,000
we can see that salaries vary randomly
(b) The plot of data and the regression line is shown in the next picture:
where x represents home runs (HR) and y represents Salary
r = 0.1369
(c) the correlation is positive (the slope of the regression line is positive) and negligible (r is near zero)
(d) The equation of the regression line is:
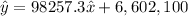
(e) Substituting with x^ = 21:
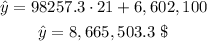
Substituting with x^ = 70:
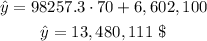
The prediction for 21 home runs is likely to be more accurate