We are given that the area of a rectangle is 150 square feet. If "h" is the height and "l" is the length then the area is given by:
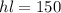
We are also given that the height is 5 feet less than twice its length, this can be written mathematically as:
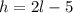
Now we can replace the value of "h" in the equation for the area:
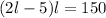
Now we use the distributive property:
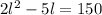
Now we have a quadratic equation that can be written as:
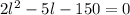
We can factor this equation to determine the values of "l". We multiply and divide by 2:
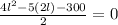
Factoring in the numerator:
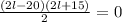
Now we take common factor in the first parenthesis in the numerator:
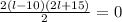
Simplifying:
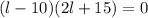
Now we set each factor to zero:
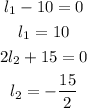
We take the positive value, therefore, the length of the rectangle is 10 feet. Now we replace this value in the equation for the height.
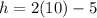
Solving we get:
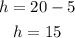
Therefore, the height of the rectangle is 15 feet.