Answer:
• AB=13cm
,
• BC=33cm
,
• CD=13cm
,
• AD=33cm
Step-by-step explanation:
The perimeter of the parallelogram = 92 cm
Let the length of side AB = x
AD is 7 more than twice AB.
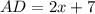
AB and AD are adjacent sides.
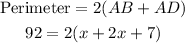
First, we solve for x:
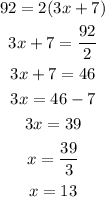
Therefore:
![\begin{gathered} AB=13\operatorname{cm} \\ AD=2x+7 \\ =2(13)+7 \\ AD=33\operatorname{cm} \end{gathered}]()
The side lengths of the parallelogram are:
• AB=13cm
,
• BC=33cm
,
• CD=13cm
,
• AD=33cm