Two triangles that are similar have the following characteristics:
1) The corresponding angles are congruent
2) The corresponding sides ratios have the same proportion.
So for triangles, JKL and J'K'L' the ratios of the corresponding sides are:
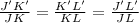
Given
JK=10cm
KL=30cm
K'L'=13.5cm
We can calculate the length of J'K' using the ratios:
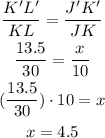
Segment J'K'=4.5cm