Question

In a bag there are green, yellow and orange marbles. The ratio of green to yellow marbles is 2 to 5. The ratio of yellow to orange marbles is 3 to 4. What is the ratio of green to orange marbles?

Answer 1

We have to simplify the ratios to make them comparable;

If the ratio of green to yellow marbles is 2 to 5 and

The ratio of yellow to orange marbles is 3 to 4.

`\begin{gathered} \text{Green to yellow = }2\colon5 \\ \text{Yellow to Orange=3 : 4} \\ \text{Multiply the gr}een\text{ yellow ratio by 3, multiply the yellow-orange ratio by 5, we obtain;} \\ \text{Green to yellow becomes = 6 : 15} \\ \text{Yellow to orange becomes = 15 : 20} \end{gathered}`

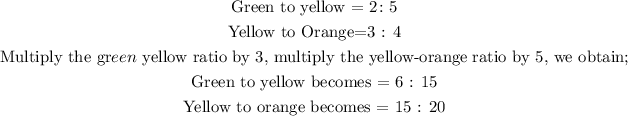
Now we can rewrite the ratios of green: yellow : orange as

`6\colon15\colon20`

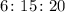
From this, we can see that the ratio of green to orange marbles is;

`\begin{gathered} 6\colon20 \\ or\text{ in simplest terms} \\ 3\colon10 \end{gathered}`

Therefore, the ratio of green to orange marbles is 3 : 10