1 Answer

Micheal · Answer 1 · 2023-11-01T23:21:05+0000

Question:

Solution:

According to the data of the problem, the series is given by the following expression:

$\sum ^(\infty)_(n\mathop=1)(n)/(3^n)=(1)/(3^1)+(2)/(3^2)+(3)/(3^3)+\cdots$

now, remember the ratio test:

Suppose we have the series

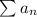
$\sum ^{}_{}a_n$

Define,

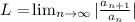
$L\text{ =}\lim _(n\to\infty)|(a_(n+1))/(a_n)|$

Then,

if L<1, the series is absolutely convergent (and hence convergent).

if

L>1, the series is divergent.

if

L=1 the series may be divergent, conditionally convergent, or absolutely convergent.

Applying this definition to the given series, we obtain:

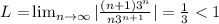
$L\text{ =}\lim _(n\to\infty)|\frac{(n+1)3^n_{}}{n3^(n+1)_{}}|=(1)/(3)<1$

then, the given series is absolutely convergent (and hence convergent). So that, we can conclude that the correct answer is:

Please log in or register to add a comment.