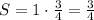Question

Can you explain the steps to letter a which is above the word solution i dont understand them

Answer 1

Given the series:

`1-(1)/(3)+(1)/(9)-...`

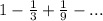
State if the series is convergent or divergent and if convergent, find its sum.

The sequence of terms forms a geometric pattern. Each term is found by multiplying the previous term by a constant number (the common ratio).

Let's find the value of the common ratio by dividing any two successive terms, for example:

`r=(-(1)/(3))/(1)=-(1)/(3)`

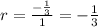
The common ratio is greater than -1 and less than 1, so the series is convergent.

Now we find the sum of the infinite series by using the formula:

`S=(t_1)/(1-r)`

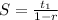
Where t1 is the first term, that is, t1 = 1.

Substituting:

`S=(1)/(1-\left(-(1)/(3)\right))`

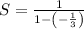
Now we add the numbers to the denominator:

`S=(1)/(1+(1)/(3))`

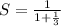
We have a sum of an integer and a fraction:

`1+(1)/(3)`

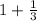
To add these numbers, we must get them to have the same denominator, thus:

`1+(1)/(3)=(3)/(3)+(1)/(3)=(4)/(3)`

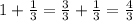
Operating:

`S=(1)/((4)/(3))`

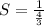
To divide by a fraction, we multiply by its reciprocal:

`S=1\cdot(3)/(4)=(3)/(4)`