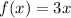Answer:
The linear equation is;
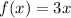
Step-by-step explanation:
Given that the function f(x) is a linear function;
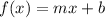
let us derive the values of m and b.
At x=-1, f(-1)=-3;
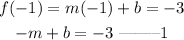
At x=2, f(2)=6;
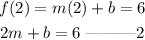
subtract equation 1 from 2;
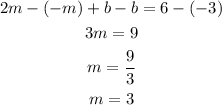
let's substitute the value of m into equation 2;
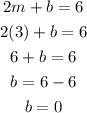
Therefore, since we have the values of m and b we can substitute to get the equation f(x);
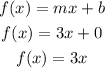
The linear equation is;