Given the functions:
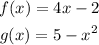
We will find (f o g)(-2)
So, first, we will find the function (f o g)(x) as follows:

Now, substitute with x = -2
so,
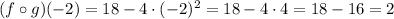
so, the answer to the part (a) (f o g)(-2) = 2
b) (g o f)(-2)
We will find (g o f)(x) as follows:
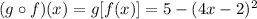
Substitute with x = -2
So,
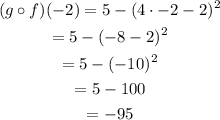
So, the answer to the part (b): (g o f)(-2) = -95