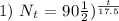
2) 5.625 mg will be left
Step-by-step explanation:
1) Half-life = 17.5 days
initial amount of Arsenic-74 = 90 mg
To get the equation, we will use the equation of half-life:
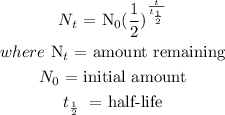
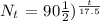
2) we need to find the remaining amount of Arsenic-74 after 70 days
t = 70
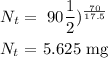
So after 70 days, 5.625 mg will be left