Question

Hey I would like to get help on this really need fast thank you.

Answer 1

We have to reflect each point of the triangles over the x-axis.

We can start by finding the algebraic expression for the rule for this type of reflection.

For any given point (x,y), when reflected across the x-axis, it will keep its x-coordinate but its y-coordinate will change sign.

Then, we can express this as a rule like:

`\lparen x,y)-->\left(x,-y\right)`

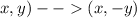
Then, we can apply this rule for each of the points as:

`\begin{gathered} J\left(-7,-7\right)-->J^(\prime)\left(-7,7\right) \\ K\left(-5,-2\right)-->K^(\prime)\left(-5,2\right) \\ L\left(-2,-3\right)-->L\left(-2,3\right) \end{gathered}`

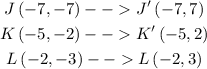
Answer:

J' = (-7, 7), K' = (-5, 2), L' = (-2, 3).

The algebraic expression is (x, y) --> (x, −y).