Question

f(x) =5x(squared) - 7x +6a) Find the coordinates of the turning point on the graph of y = f(x).b) Show that the turning point is a minimum point.

Answer 1

Given:

`f\mleft(x\mright)=5x^2-7x+6`

To find:

a) The coordinates of the turning point on the graph of y = f(x).

b) Show that the turning point is a minimum point.

Step-by-step explanation:

a) Using the first derivative test,

`\begin{gathered} f^(\prime)(x)=0 \\ 10x-7=0 \\ x=(7)/(10) \end{gathered}`

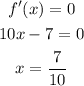
Substituting in the given function we get,

`\begin{gathered} f((7)/(10))=5((7)/(10))^2-7((7)/(10))+6 \\ =(71)/(20) \end{gathered}`

Therefore, the turning point is,

`((7)/(10),(71)/(20))`

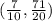
b) Differentiating with respect to x again,

`f^(\prime)^(\prime)(x)=10>0`

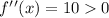
Therefore, the function has a minimum value at the turning point.

Hence, the turning point is a minimum point.