Question

50"40DmZCDE =65mZDCA =75 answer choices:6575502540note** i put in what i think is correct but im not sure it seems wrong.

Answer 1

In triangle CDE, the sides CD is equal to side CE, so angle opposite to side CD is equal to angle opposite to side CE, means

`\angle CDE=\angle CED`

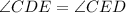
Determine the measure of angle CDE (or angle CED) by using angle sum property of triangle.

`\begin{gathered} \angle CDE+\angle CED+\angle DCE=180 \\ \angle CDE+\angle CDE+50=180 \\ 2\angle CDE=180-50 \\ \angle CDE=(130)/(2) \\ \angle CDE=65 \end{gathered}`

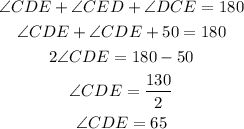
The measure of angle CDE is 65 degrees.

The angle CDE and angle CDA are linear pair of angles. So,

`\angle CDE+\angle CDA=180`

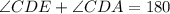
Substitute the measure of angle CDE to obtain the measure of angle CDA.

`\begin{gathered} 65+\angle CDA=180 \\ \angle CDA=180-65 \\ =115 \end{gathered}`

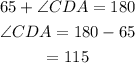
Consider the triangle CAD.

Determine the measure of angle DCA by using angle sum property of triangle.

`\begin{gathered} \angle CAD+\angle CDA+\angle DCA=180 \\ 40+115+\angle DCA=180 \\ \angle DCA=180-155 \\ =25 \end{gathered}`

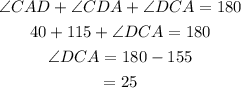
So measure of angle DCA is 25 degrees.