Given the function:
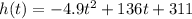
Given that NASA launches a rocket at t= 0 seconds.
Where h is the height in meters above sea level.
Let's solve for the following:
• (a). The time the rocket splashes the water.
When the rocket splashes the water, the height above sea-level will be 0 meters.
To solve for t, set h(t) for 0 and solve.
We have:
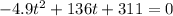
Now, let's solve using the quadratic formula:
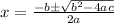
Where:
a = -4.9
b = 136
c = 311
Plug in the values into the formula and solve for t:
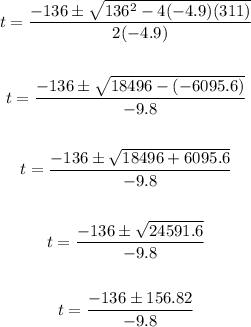
Solving further:
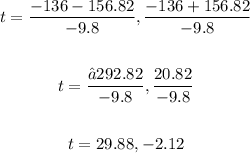
Thus, we have the solutions:
t = 29.88 and t = -2.12
Since the time cannot be negative, let's take the positive solution.
Therefore, the rocket splashes down after 29.88 seconds.
• (b). Let's find the peak.
To find the maximum time, apply the fomula:
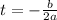
Thus, we have:
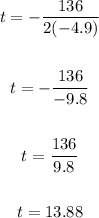
The rocket gets to its peak at 13.88 seconds.
Now, to find the height at that time, substitute 13.88 for t in h(t) and solve for h(13.88):

Therefore, the rocket peaks at 1254.67 above seal level.
ANSWER:
• 29.88 seconds
• 1254.67 meters