Question

The PTO is selling raffle tickets to raise money for classroom supplies. A raffle ticket costs $4. There is 1 winning ticket outof the 170 tickets sold. The winner gets a prize worth $98. Round your answers to the nearest centWhat is the expected value (to you) of one raffle ticket? SiCalculate the expected value to you) if you purchase 10 raffle tickets. SWhat is the expected value (to the PTO) of one raffle ticket? $If the PTO sells all 170 raffle tickets, how much money can they expect to raise for the classroom supplies? s

Answer 1

First, we find the probability of winning a ticket

`P=(1)/(170)`

Now, we find the probability of losing

`P=(169)/(170)`

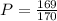
We know that we can lose -$4, which is the cost of the ticket. But, we can win $94, those are the scenarios.

`98-4=94`

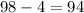
Now, we use all this information to find the expected value, which is the summary of the products between each outcome value and its probability, which includes winning or losing events.

`\begin{gathered} E=94\cdot(1)/(170)+(-4)\cdot(169)/(170) \\ E=(94)/(170)-(676)/(170)=(94-676)/(170)=-(582)/(170) \\ E\approx-3.42 \end{gathered}`

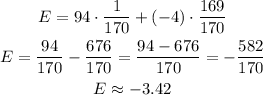
Therefore, the expected value of one raffle ticket is -3.42.

Next, if we buy 10 raffle tickets, then we have to multiply it by -3.42

`-3.42\cdot10\approx-34.2`

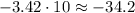
The expected value if we purchase 10 raffle tickets is -34.2.

Now, the PTO has an expected value that is opposite to the person who buys raffles tickets because if the buyer wins, then the PTO loses the same amount of money. This means that the expected value of the PTO of one raffle ticket is $3.42.

Then, if the PTO sells 170 raffle tickets, they would be expected

`170\cdot3.42=581.40`

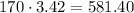
Therefore, the PTO expects to raise $581.40 if they sell 170 raffle tickets.