Given the function:
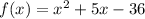
Let's find the zeros of the function.
To find the zeros, substitute 0 for f(x) and solve for x.
We have:
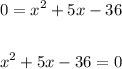
Factor the expression using the AC method.
Find a pair of intergers whose sum is 5 and whose product is -36.
We have:
-4 and 9
Thus, we have the factors:
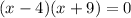
Now, equate each factor to zero and solve for x:

We have the solutions:
x = 4 and -9
Therefore, the zeros of the function are: 4 and -9
ANSWER:
A) 4 and -9