Question

Graphing Quadratic-Quadratic Systems.GGWhich of the following graphs represents the solution(s) of the following system?2+y=7P + y = 49+00身並查非DONE

Answer 1

The system of equations is given to be:

`\begin{gathered} x^2+y=7^{} \\ x^2+y^2=49 \end{gathered}`

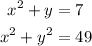
The first equation is a quadratic equation in the form:

`y=-x^2+7`

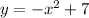
The coefficient of x² is negative. Therefore, the graph opens downwards.

The second equation is a circle in the form:

`(x-h)^2+(y-k)^2=r^2`

Comparing the equation we have, we know that the circle has a radius of:

`\begin{gathered} r=\sqrt[]{49} \\ r=7 \end{gathered}`

Using a graphing tool, we can draw the graph to confirm the answer. This is shown below:

Hence, the SECOND OPTION is correct.