Question

Mark throws a ball upward at 64 feet per second. Sean is on top of a building 48 feet in height. He catches the ball on the way down. A) how long was the ball in the air?B)how high did the ball go?

Answer 1

ANSWERS

(a) 3 seconds

(b) 63.66 feet

Step-by-step explanation

First we have to find how long does it take for the ball to reach its maximum height, which will allow us to find what is that maximum height. That way we will be able to determine the time until Sean catches the ball on the way down.

We know that when the ball reaches its maximum height, its velocity is zero - this is because the ball stops for a moment before changing its direction. Thus we have the final velocity after a time t,

`v=u-gt`

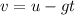
u is the initial velocity, u = 64 ft/s and g = 9.81m/s². At the maximum height v = 0. But first we have to change the meters into feet, knowing that 1m = 3.28 ft,

`9.81(m)/(s^2)\cdot(3.28ft)/(1m)\approx32.17ft/s^2`

Back to the equation for velocity,

`0=64ft/s-32.17ft/s^2\cdot t_(\max )`

Solving for tmax,

`t_(\max )=(64ft/s)/(32.17ft/s^2)\approx2s`

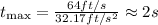
This means that initially, the ball was in the air for 2 seconds while going upward.

The height of the ball at this time is determined by the equation,

`y_(\max )=u\cdot t_(\max )-(1)/(2)gt^2_(\max )`

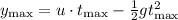
Replacing the values,

`y_(\max )=64(ft)/(s)\cdot2s-(1)/(2)\cdot32.17(ft)/(s^2)\cdot2^2s^2`
`y_(\max )=63.66ft`

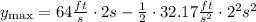
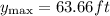
The ball went 63.66 ft before coming down.

Now, Sean catches the ball at a height of 48 feet,

`63.66ft-48ft=15.66ft`

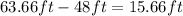
Sean is 15.66 ft below the maximum height of the ball. We know that when it comes down, the ball has initial velocity of zero - remember it changes its direction, so the vertical displacement is,

`\Delta y=(1)/(2)gt^2_{\text{sean}}`

We have to find the time from the maximum height until Sean catches the ball,

`t_{\text{sean}}=\sqrt[]{(\Delta y\cdot2)/(g)}`
`t_{\text{sean}}=\sqrt[]{(15.66ft\cdot2)/(32.17ft/s^2)}\approx1s`

So if it took 2 seconds for the ball to reach its maximum height and then another 1 second for Sean to catch it, then,

`2s+1s=3s`

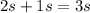
This means that the ball was in the air for a total time of 3 seconds.