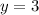We have the following:
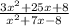
factoring:
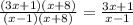
now, the horizontal asymptote is:
if denominator degree> numerator degree, the horizontal asymptote is the x-axis: y = 0
if the degree of the numerator = 1 + the degree of the denominator, the slanted asymptote of the form y = mx + b
if the degrees are equal, the asymptote is the quotient of the principal coefficients of the numbered and denoninator, therefore
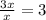
Therefore the horizontal asymptote is