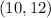Question

Points A, B and C are collinear, and AB : BC = 1: 4. A is located at (-5, - 3), B is located at (-2, 0) and C is located at (I, 1), on the directedsegment AC. What are the values of x and y?A(7,9)B(10,12)C(20,18)D(-4.4,-2.4)

Answer 1

From the question

We are given the points

`A(-5,-3),B(-2,0),C(x,y)`

Where points A, B, C are collinear points

We are given that

`\bar{AB}\colon\bar{BC}=1\colon4`

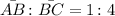
Since the points are collinear then

by the ratio rule, we have

`((bx_1+ax_2)/(a+b),(by_1+ay_2)/(a+b))=(-2,0)`

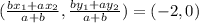
Where

a = 1, b = 4

Also

`\begin{gathered} x_1=-5,x_2=x \\ y_1=-3,y_2=y \end{gathered}`

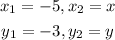
Hence we have

`((4(-5)+1(x))/(4+1),(4(-3)+y)/(4+1))=(-2,0)`

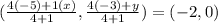
Simplifying this we get

`(-(20+x)/(5),(-12+y)/(5))=(-2,0)`

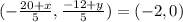
This implies

`\begin{gathered} (-20+x)/(5)=-2 \\ -20+x=-10 \\ x=-10+20 \\ x=10 \end{gathered}`

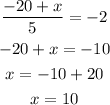
Also we have

`\begin{gathered} (-12+y)/(5)=0 \\ y=12 \end{gathered}`

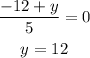
Therefore, x = 10, y = 12

Hence the solution is

`(10,12)`