Given:
The line passing through the points (1,5) and (-5,2).
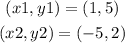
Required:
To find the equation of line, x- and y-intercepts.
Step-by-step explanation:
The general form of line equation is
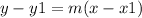
Here
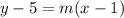
Where m is the slope.
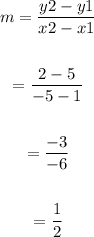
Therefore the equation of line is
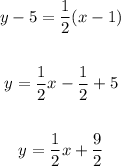
Here the x-intercept is
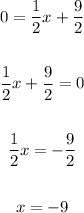
And the y-intercept is,
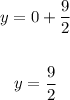
Final Answer:
The line equation is :
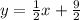
The x-intercept is :( -9,0)
The y-intercept is : (0,9/2)