Question

Find g(x) if the indefinite integral of f(x) need little help

Answer 1

g(x) = 4x² - x

General Formulas and Concepts:

Algebra II

Functions

• Function Notation
• Piecewise Functions

Calculus

Integration

• Integrals
• Integral Notation
• Integration Constant C

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

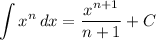
Integration Property [Multiplied Constant]:
`\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx`

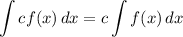
Integration Property [Addition/Subtraction]:
`\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx`

Explanation:

*Note:

Integrating a piecewise function requires you to integrate both parts.

Step 1: Define

Identify.

`\displaystyle f(x) = \left \{ {{8x - 1 ,\ x \leq 4} \atop {31 ,\ x \geq 4}} \right.`

`\displaystyle \int {f(x)} \, dx = \left \{ {{g(x) + C ,\ x \leq 4} \atop {31x + C ,\ x \geq 4}} \right.`

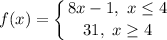
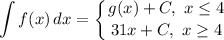
Step 2: Find function g(x)

We can see that the 2nd part of the piecewise function already has been integrated:

1. [Integral] Set up:
   `\displaystyle \int {f(x)} \, dx ,\ x \geq 4 = \int {31} \, dx ,\ x \geq 4`
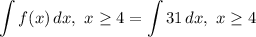
2. [Integral] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int {f(x)} \, dx ,\ x \geq 4 = 31 \int {} \, dx ,\ x \geq 4`
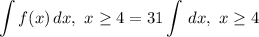
3. [Integral] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle \int {f(x)} \, dx ,\ x \geq 4 = 31x + C ,\ x \geq 4`

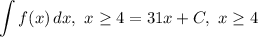
To find function g(x), we simply have the same setup:

1. [Integral] Set up:
   `\displaystyle \int {f(x)} \, dx ,\ x \leq 4 = \int {8x - 1} \, dx ,\ x \leq 4`
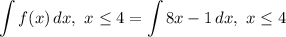
2. [Integral] Rewrite [Integration Rule - Addition/Subtraction]:
   `\displaystyle \int {f(x)} \, dx ,\ x \leq 4 = \int {8x} \, dx - \int {1} \, dx ,\ x \leq 4`
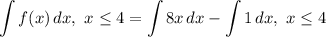
3. [Integrals] Rewrite [Integration Property - Multiplied Constant]:
   `\displaystyle \int {f(x)} \, dx ,\ x \leq 4 = 8 \int {x} \, dx - \int {} \, dx ,\ x \leq 4`
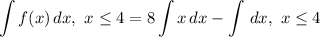
4. [Integrals] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle \int {f(x)} \, dx ,\ x \leq 4 = 8 \bigg( (x^2)/(2) \bigg) - x + C ,\ x \leq 4`
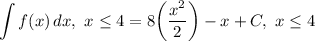
5. Simplify:
   `\displaystyle \int {f(x)} \, dx ,\ x \leq 4 = 4x^2 - x + C ,\ x \leq 4`
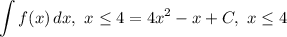
6. Redefine:
   `\displaystyle g(x) = 4x^2 - x + C ,\ x \leq 4`

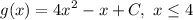
The integration constant C is already included in the answer, so our answer is g(x) = 4x² - x.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration (Applications)