Question

Quadratic Equations:Find the values of a, b, & c, that should be used in the quadratic formula to determine the solution. This will be a 2 step problem.Step 1 of 2: -2y^2 + y + 7 = 0what is a =what is b=what is C=w

Answer 1

Given the following quadratic equation:

`\text{ -2y}^2\text{ + y + 7 = 0}`

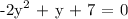
The given equation is already in standard form a^2y + by + c = 0. Thus, we can say that a, b and c values are the constants of each term.

Therefore,

a = -2

b = 1

c = 0

To be able to determine the solution, we will be using the following formula:

`\text{ y = }\frac{-b\text{ }\pm\text{ }\sqrt[]{b^2-4ac}}{2a}`

Plugging in the values of a, b and c, we get:

`\text{ y = }\frac{-1\text{ }\pm\text{ }\sqrt[]{(1)^2-4(-2)(0)}}{2(-2)}`
`\text{ y = }\frac{-1\text{ }\pm\text{ }\sqrt[]{1-0)}}{-4}`
`\text{ y = }\frac{-1\text{ }\pm\text{ }\sqrt[]{1}}{-4}`
`\text{ y = }\frac{-1\text{ }\pm\text{1}}{-4}`
`y_1\text{ = }\frac{-1\text{ + 1}}{-4}\text{ = }(0)/(-4)\text{ = 0}`
`y_2\text{ = }\frac{-1\text{ - 1}}{-4}\text{ = }(-2)/(-4)\text{ = }(2)/(4)\text{ = }(1)/(2)\text{ or 0.5}`

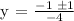
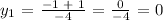
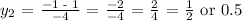
Therefore, the solutions of the given quadratic equation are y = 0 and y = 1/2 or 0.5. It has two different solutions.