Let us first review what we are given in the problem:
the game costs $1.35
3 digits are to be selected from 0 to 9
repetition is allowed (based on the given example)
a winning sequence earns $477.75
a. How many different selections are possible?
There are three slots and each slot has 10 digits to choose from. So there are 10 x 10 x 10 = 1,000 possible selections (from 000 up to 999)
b. What is the probability of winning?
The probablity of winning is equal to the number of ways you can win, divided by the total number of possible selections. Since there is ony one sequence that will win, then the answer is 1/1,000 or 0.001.
c. If you win, what is your net profit?
If you win, then your profit is equal to $477.75 minus the cost of joining the game, which is $1.35. So your profit is $476.40.
Note that if you do not win, then you lose the $1.35 you paid for joining the game.
d. Find the expected value.
The expected value is equal to the summation of all the possible outcomes (profits or losses) multiplied by their corresponding probabilities. So we calculate it as follows:
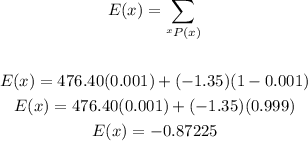
The expected value is -0.87 or a loss of $0.87.