Question

A billiard ball of mass 0.500 kg moves at a velocity of 2.20m/s [fwd] when it collides elastically with asecond ball, of mass 0.350 kg. The second ball is initially moving at 1.50m/s [fwd]. Determine theobtained velocity of both balls after the collision.

Answer 1

Given:

The mass of the 1st ball, m₁=0.500 kg

The velocity of the 1st ball before the collision, u₁=2.20 m/s

The mass of the 2nd ball, m₂=0.350 kg

The speed of the second ball before the collision, u₂=1.50 m/a

To find:

The velocities of the balls after the collision.

Step-by-step explanation:

In an elastic collision, both momentum and the kinetic energies of the balls are conserved.

The velocities of the balls after the collision are given by,

`\begin{gathered} v_1=(m_1-m_2)/(m_1+m_2)u_1+(2m_2)/(m_1+m_2)u_2\text{ }\to\text{ \lparen i\rparen} \\ v_2=(2m_1)/(m_1+m_2)u_1+(m_2-m_1)/(m_1+m_2)u_2\text{ }\to\text{ \lparen ii\rparen} \end{gathered}`

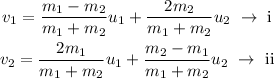
Where v₁ is the velocity of the 1st ball and v₂ is the velocity of the 2nd ball.

On substituting the known values in equation (i),

`\begin{gathered} v_1=(0.500-0.350)/(0.500+0.350)*2.20+(2*0.350)/(0.500+0.350)*1.50 \\ =1.62\text{ m/s} \end{gathered}`

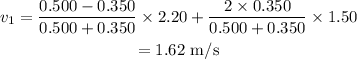
On substituting the known values in the equation (ii),

`\begin{gathered} v_1=(2*0.500)/(0.500+0.350)*2.20+(0.350-0.500)/(0.500+0.350)*1.50 \\ =2.32\text{ m/s} \end{gathered}`

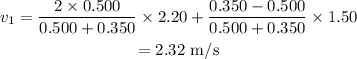
Final answer:

The velocity of the 1st ball is 1.62 m/s after the collision.

The velocity of the 2nd ball after the collision is 2.32 m/s.