Question

I'm unsure of the best way to approach this exponential word problem and turn it into a functional equation

Answer 1

From the question;

A sample of bacteria is growing at an hourly rate of 6%

This means

Rate of growth = 6%

The sample began with 15 bacteria

We are to find how many bacteria will be in the sample after 18 hours

This will be done by using exponential growth formula

`A=P(1+(r)/(100))^{t^{}}`

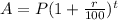
Where

p = initial number of bacteria

r = rate of growth

t = time

A = new number of bacteria

From the question

`p=15,r=6\text{\%, t = 18, }`

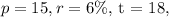
Hence we have

`A=15(1+(6)/(100))^(18)`

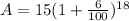
By simplifying further we have

`\begin{gathered} A=15(1+0.06)^(18) \\ A=15(1.06)^(18) \\ A=15(2.854) \\ A=42.815 \\ A=43(to\text{ the nearest whole number)} \end{gathered}`

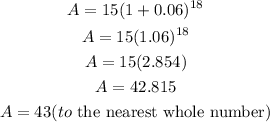
Therefore,

There will be 43 bacteria after 18 hours