Question

The area of a playground is 140 yd^2. The width of the playground is 4 yd longer than its length. Find the length and width of the playground.

Answer 1

The area of a rectangle is the width multiplied by its length:

So we have that the area is:

`140=W\cdot L=(L+4)L=L^2+4L`

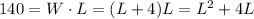
We can use this formula to find the length:

`ax^2+bx+c=0\Rightarrow x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

If we put 140 in the other term we have a similar expression with L instead of x:

`L^2+4L-140=0`

We have that a=1, b=4 and c=-140

`L=\frac{-4\pm\sqrt[]{4^2+4\cdot140}}{2}=\frac{-4\pm\sqrt[]{16+560}}{2}=(-4\pm24)/(2)`

We get 2 results from here: L= -14yd and L = 10yd. Since the length can't be negative, we found that the length of the playground is 10 yd.

Then, we had that the width is 4yd longer that the length, so the width of the playground is 14 yd