Given,
The coodinates of the points are P(7,7).
The scale factor is 1/2.
The coordinates of center of dilation is (1,3).
In the operation described here, it is the vector (center of dilation→ similar point) that will get multiplied by a factor 1/2.
The vector from the centre (1,3) to point (7,7) has coordinates (7,7) - (1,3)

Now, dilated the coordinates by the scale factor of 1/2 then,

Image of the point is at,
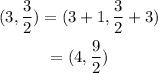
Hence, the coordinates of the image is (4,9/2).