Question

Three cards are drawn with replacement from a standard deck of 52 cards. Find the the probability that the first card will be a spade, the second card will be a red card, and the third card will be a face card. Express your answer as a fraction in lowest terms or a decimal rounded to the nearest millionth.

Answer 1

Given:

The total cards is: 52

Number of spade cards: 13

Number of red cards: 26

Number of face cards: 12

Therefore,

`P(\text{spade)}=(13)/(52)=(1)/(4)`
`P(red)=(26)/(52)=(1)/(2)`
`P(\text{face)}=(12)/(52)=(3)/(13)`

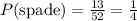
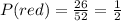
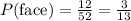
The probability that the first card will be a spade, the second card will be a red card, and the third card will be a face card is given by:

`P(spade\text{ and red and face)=P(spade)}\cdot P(red)\cdot P(face)`

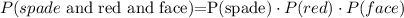
Substitute:

`=(1)/(4)\cdot(1)/(2)\cdot(3)/(13)=(1\cdot1\cdot3)/(4\cdot2\cdot13)=(3)/(104)`

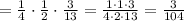
Answer: 3/104