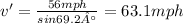Question

A pilot wants to fly on a bearing of 69.2°. By flying due east, he finds that a 56mph wind, blowing from the south, puts him on course. Find the airspeed of the plane.

Answer 1

Take into that the given situation can be illustrated as follow:

In the previous image, red line respresents the speed and direction of the ariplane, black line represents the speed and direction of the wind and green line represents the resultant direction of the airplane due to the influence of the wind.

As you can notice, the previous situation is illustrated with a right triangle. By using the tan69.2°, you have:

`tan69.2°=(opposite)/(adjacent)=(56mph)/(v)`

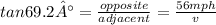
opposite is 56mph and adjacent makes reference to the airplane speed v. By solving for v and by simplifying you get:

`v=(56mph)/(tan69.2)=22.4mph`

Hence, the speed of the airplane to the east is 22.4mph.

The resultant speed if the airplane under the influence of the wind is (green line):

`v^(\prime)=(56mph)/(sin69.2°)=63.1mph`