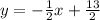Question

Find the equation that passes through the points (1,6) and (5,4)

Answer 1

To find the equationof a line that passes through 2 given points, we use the following steps:

1 - given point (x1, y1) and (x2, y2), find the slope "s":

`s=(y_2-y_1)/(x_2-x_1)`

2 - Using the slope and one of the given points, write the equation in the slope-point form:

`(y-y_1)=s(x-x_1)`

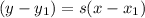
3 - Solve fo "y" to get the slope-intercept form as an answer.

So:

1 - Find the slope:

`s=(4-6)/(5-1)=(-2)/(4)=-(1)/(2)`

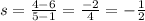
2 - Write the slope-point form:

`(y-6)=-(1)/(2)(x-1)`

3 - Solve for y:

`\begin{gathered} y-6=-(1)/(2)x+(1)/(2) \\ y=-(1)/(2)x+(1)/(2)+6 \\ y=-(1)/(2)x+(1+12)/(2) \\ y=-(1)/(2)x+(13)/(2) \end{gathered}`

So, the equation of the line is:

`y=-(1)/(2)x+(13)/(2)`