SOLUTION:
Step 1 :
In this question, we are told that a marketing research company needs to estimate the average total compensation of CEOs in the service industry.
We also have that: Data were randomly collected from 38 CEOs and the 98% confidence interval was calculated to be ($2,181,260, $5,836,180).
Then, we are asked to find the margin error for the confidence interval.
Step 2:
We need to recall that:
![\text{Higher Confidence Interval, CI}_{H\text{ = }}X\text{ + }\frac{Z\sigma}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/2kdw8hjfye8hvnil8v7ohzxmxg4fqkr2k3.png)
![\text{Lower Confidence Interval , CI}_{L\text{ }}=\text{ X - }\frac{Z\sigma}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/wzg49e2n38isczm25o9fyhqkixzh5ol1uq.png)
It means that:
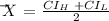
![\text{Margin of error, }\frac{Z\sigma}{\sqrt[]{n}\text{ }}\text{ = }\frac{CI_{H\text{ - }}CI_L}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/a8d5a942ykvvromtb2una2xdyn7cv7lqed.png)
where,
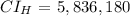
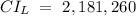
putting the values into the equation for the margin of error, we have that:
![\text{Margin of error,}\frac{Z\sigma}{\sqrt[]{n}\text{ }}\text{ = }\frac{5,836,180\text{ - }2,181,260\text{ }}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/v67zypp0u9kyeqhef5geebwp0u7ki8p3k8.png)
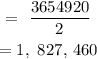
CONCLUSION:
The margin error for the confidence interval is 1, 827, 460