Question

) f) 1 + cot²a = cosec²a​

Answer 1

It is an identity, proved below.

Explanation:

I assume you want to prove the identity. There are several ways to prove the identity but here I will prove using one of method.

First, we have to know what cot and cosec are. They both are the reciprocal of sin (cosec) and tan (cot).

`\displaystyle \large{\cot x=(1)/(\tan x)}\\\displaystyle \large{\csc x=(1)/(\sin x)}`

csc is mostly written which is cosec, first we have to write in 1/tan and 1/sin form.

`\displaystyle \large{1+((1)/(\tan x))^2=((1)/(\sin x))^2}\\\displaystyle \large{1+(1)/(\tan^2x)=(1)/(\sin^2x)}`

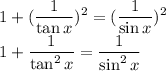
Another identity is:

`\displaystyle \large{\tan x=(\sin x)/(\cos x)}`

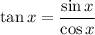
Therefore:

`\displaystyle \large{1+(1)/(((\sin x)/(\cos x))^2)=(1)/(\sin^2x)}\\\displaystyle \large{1+(1)/((\sin^2x)/(\cos^2x))=(1)/(\sin^2x)}\\\displaystyle \large{1+(\cos^2x)/(\sin^2x)=(1)/(\sin^2x)}`

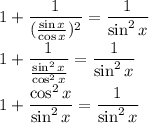
Now this is easier to prove because of same denominator, next step is to multiply 1 by sin^2x with denominator and numerator.

`\displaystyle \large{(\sin^2x)/(\sin^2x)+(\cos^2x)/(\sin^2x)=(1)/(\sin^2x)}\\\displaystyle \large{(\sin^2x+\cos^2x)/(\sin^2x)=(1)/(\sin^2x)`

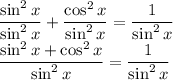
Another identity:

`\displaystyle \large{\sin^2x+\cos^2x=1}`

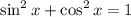
Therefore:

`\displaystyle \large{(\sin^2x+\cos^2x)/(\sin^2x)=(1)/(\sin^2x)\longrightarrow \boxed{ (1)/(\sin^2x)={(1)/(\sin^2x)}}`

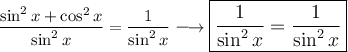
Hence proved, this is proof by using identity helping to find the specific identity.