1 Answer

Rob Volk · Answer 1 · 2023-12-26T15:09:29+0000

First, we need to calculate the area of the whole circle.

The area of a circle is computed as follows:

$A=\pi r^2$

The radius of circle F is EF = 14.

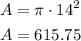
$\begin{gathered} A=\pi\cdot14^2 \\ A=615.75 \end{gathered}$

This area corresponds to 360°. To find the area that corresponds to 144°, we can use the next proportion:

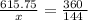
$(615.75)/(x)=\frac{360\text{ \degree}}{144\text{ \degree}}$

Solving for x,

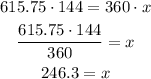
$\begin{gathered} 615.75\cdot144=360\cdot x \\ (615.75\cdot144)/(360)=x \\ 246.3=x \end{gathered}$

The area of sector EFG is 246.3

Please log in or register to add a comment.