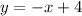Question

QuestionDetermine the equation of the line passing through the points (3, 1) and (5, -1).Write the linear equation in slope-intercept formy = mx +b.

Answer 1

Given the points (3, 1) and (5, -1)

we will write the equation of the line using the slope-intercept form:

`y=mx+b`

Where (m) is the slope and (b) is the y-intercept

The slope will be calculated as follows:

`\begin{gathered} slope=(rise)/(run)=(y_2-y_1)/(x_2-x_1) \\ \\ m=(-1-1)/(5-3)=(-2)/(2)=-1 \end{gathered}`

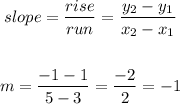
substitute with m into the equation of the line:

`y=-x+b`

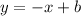
Substitute with point (3, 1) to find the value of (b)

`\begin{gathered} 1=-3+b \\ b=1+3=4 \end{gathered}`

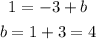
Substitute with (m) and (b) into the equation of the line

So, the answer will be:

`y=-x+4`