Step-by-step explanation:
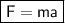
The Newton's Second law of motion, also known as The Law of mass and acceleration, derives the given equation in terms of mass, acceleration and force.
It actually states that Force applied on a body is equal to the time rate of change of it's momentum.
Momentum of a body, is the product of it's mass and velocity with which its moving.
This clarifies that objects at rest have zero momentum since they have zero velocity.
If a "source" applies force on an object, it's magnitude would depend on its rate of change of momentum with time.
Since, mass of an object is a fixed entity, so change in momentum would be caused due to change in velocity.
Now, if we happen to have two objects of different mass,
(As, in here, a chair and a large couch) and we have to push them so as to produce the same change in momentum, the force applied on a couch would be more than that applied on the chair.
Answer:
This is simply because,
Force = mass × acceleration
If acceleration for both the objects is fixed, the force applied differs due to theur difference in mass.
Note here that Force I'd directly proportional to mass.
The greater the mass is, the higher is the force required to produce same acceleration.
Thus, objects with higher mass will require a greater amount of force to have the same acceleration as the object of light weight.