Answer:
B(5,3)
Step-by-step explanation:
Given a line segment AB with endpoints A and B defined below, the midpoint, M is obtained using the formula:
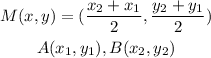
Given that:
• Midpoint=M(3,1)
,
• Coordinates of A are (1, -1)
Substitution into the formula gives:

Therefore, the coordinates of B are (5,3).