Given the functions f and g:
![\begin{gathered} f(x)=x+1 \\ g(x)=\sqrt[]{x+2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/z92stunw3vzvqfyx6pi5kc5qcf70cmdgm4.png)
to find the composition (g o f)(x), we can write the following:
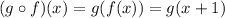
if we evaluate x+1 on g(x), we get:
![\begin{gathered} g(x+1)=\sqrt[]{(x+1)+2}=\sqrt[]{x+1+2}=\sqrt[]{x+3} \\ \Rightarrow(g\circ f)(x)=\sqrt[]{x+3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x61bcm3rf1f1yw9ztndymakd0adfkxmfgk.png)
now, notice that the composition is not defined on the real numbers that are less than -3 (sice we would get a negative inside the square root), therefore, the domain is:
![\begin{gathered} (g\circ f)(x)=\sqrt[]{x+3} \\ D=\lbrack-3,\infty) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xz2ibm5qadzokbqno95nqt9mewueq6r5bn.png)