Question

A spinner has regions numbered 1 through 21. What is the probability that the spinner will stop on an even number or a multiple of 3?A. 10/9B. 2/3C. 1/7D. 1/3

Answer 1

Let us define probability.

Probability is a mathematical tool used to study randomness. It deals with the chance or the likelihood of an event, E occurring from a sample space, S. This can be represented mathemaically as shown below

`\begin{gathered} P_r(E)=(n(E))/(n(S)) \\ \text{where } \\ P_r(E)\text{ is the probability of an event E occuring} \\ n(E)\text{ is the number of element in the Event E} \\ n(S)\text{ is the number of element in the sample space S} \end{gathered}`

From the given question, the sample space has the following elements

`\begin{gathered} S=\mleft\lbrace1,2,3,4,\ldots,21\mright) \\ n(S)=21 \end{gathered}`

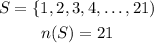
The elements of the events that the spinner would stop at an even number or a multiple of 3 would be

`\begin{gathered} \text{even number between 1 and 21 are 2,4,6,8,10,12,14,16,18,20} \\ mul\text{ltiple of 3 betwen 1 and 21 are 3,6,9,12,15,18,21} \\ \text{elements of the events would be} \\ E=\mleft\lbrace2,3,4,6,8,9,10,12,14,15,16,18,20,21\mright) \\ n(E)=14 \end{gathered}`

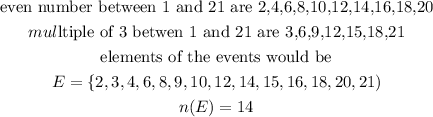
Therefore, the probability that the spinner will stop on an even number or a multiple of 3 would be

`\begin{gathered} P_r(E)=(n(E))/(n(S))=(14)/(21) \\ P_r(E)=(2)/(3) \end{gathered}`

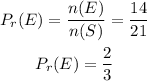
Hence, the probability that the spinner will stop on an even number or a multiple of 3