Question

I need the answers to these questions answered mathmatically. TY

Answer 1

A) From the table, value A is in the intersection between 'Like chocolate cake' and 'Like cheesecake'; therefore A is the number of people who like both chocolate cake and cheesecake.

Similarly, in the case of B, C,..., I

`\begin{gathered} A\rightarrow\text{ like chocolate cake and cheesecake} \\ B\rightarrow\text{ like chocolate cake but not cheesecake} \\ C\rightarrow\text{ Total number of people who like chocolate cake} \end{gathered}`
`\begin{gathered} D\rightarrow\text{ People who like cheesecake but not chocolate cake} \\ E\rightarrow\text{ people who do not like either chocolate cake or cheesecake} \\ F\rightarrow\text{ People who do not like chocolate cake} \end{gathered}`
`\begin{gathered} G\rightarrow\text{ People who like cheesecake} \\ H\rightarrow\text{ People who do not like cheesecake} \\ I\rightarrow\text{ Total number of surveyed people} \end{gathered}`

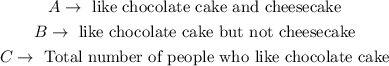
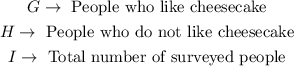
B) From part B, value E corresponds to the number of people who do not like either chocolate cake or cheesecake.

Thus, the answer to part B) is

`(E)/(I)*100\%`

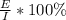
Notice that E/I alone is a decimal number.

C) We cannot know without the explicit values of the constants. Value E could be equal to 0 or close to I.