Question

A human cannonball is launched from a cannon at 20 m/s at 45° above the horizontal. What is the range of

the human cannonball?

Answer 1

Range is 57.723 m

Step-by-step explanation:

- From first newton's equation of motion;

`{ \boxed{ \pmb{v = u + gt} }}`

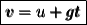
• v is final velocity
• u is initial velocity
• g is acceleration due to gravity
• t is time taken to reach maximum height

At maximum height reached; v = 0 [vertical motion], g is negative because velocity decreases as height is increasing

`{ \tt{v = u + gt}} \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \\ { \tt{0 = u \sin( \theta) + ( - g)t}} \\ { \tt{u \sin( \theta) = gt }} \: \: \: \: \: \: \: \: \: \: \: \: \: \\ \\ { \tt{t = (u \sin( \theta) )/(g) }} \: \: \: \: \: \: \: \: \: \: \: \: \: \:`

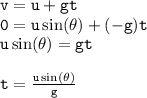
- Therefore, to get total time of flight, T;

`{ \tt{T = (2u \sin( \theta) )/(g) }} \\`

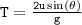
- For horizontal motion; g = 0. Consider second equation of motion;

`{ \tt{s = ut + (1)/(2) {gt}^(2) }} \\`

Let range be R

`{ \tt{R = uT + (1)/(2) (0)T}} \\ \\ { \tt{R = uT}} \\ \\ { \boxed{ \tt{R = \frac{2 {u}^(2) \sin( \theta) }{g} }}}`

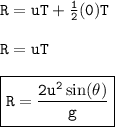
- Above is the formular of finding range;

From the question, u = 20 m/s and theta = 45°

`{ \tt{R = \frac{2(20) {}^(2) \sin(45 \degree) }{9.8} }} \\ \\ { \tt{R = (400 √(2) )/(9.8) }} \\ \\ { \tt{R = 57.723 \: m}}`